Pythonの標準ライブラリrandomで正規分布の乱数を生成する

Pythonで乱数を得るには標準ライブラリの random を使うのが一般的ではないでしょうか。正規分布（ガウス分布）に従う乱数を得るのもNumPyやSciPyなどを使う必要はなく、標準ライブラリで実現可能です。

コード

標準ライブラリの中の random.gauss() 関数を使います。

import random

r = random.gauss(mu=0.0, sigma=1.0)

参考: https://docs.python.org/ja/3/library/random.html#random.gauss

ここで mu は平均（$\mu$）、sigma は標準偏差（$\sigma$）です。

μとσの設定

標準偏差は$\mu$と$\sigma$という２つのパラメータにより定義されます。$\mu$は平均なのでわかりやすいかと思います。正規分布の山の真ん中がどこに来るかですね。$\sigma$は山の広がり具合を表します。詳細は省きますが、広がり具合の目安として確率分布関数は以下の性質を持ちます。

$\mu \pm \sigma$ の範囲にある確率が約68%
$\mu \pm 2 \sigma$ の範囲にある確率が約95%
$\mu \pm 3 \sigma$ の範囲にある確率が約99.7%

実行例

以下は $\mu = 0.0$、$\sigma = 1.0$ で生成した数のヒストグラムです。サンプル数が増えるほど綺麗な山型になるのがわかります。また $\mu \pm 3 \sigma = \pm 3$ の範囲にほぼすべて（理論上は約99.7%）が収まるというのも実感できるかと思います。

サンプル数: 1000

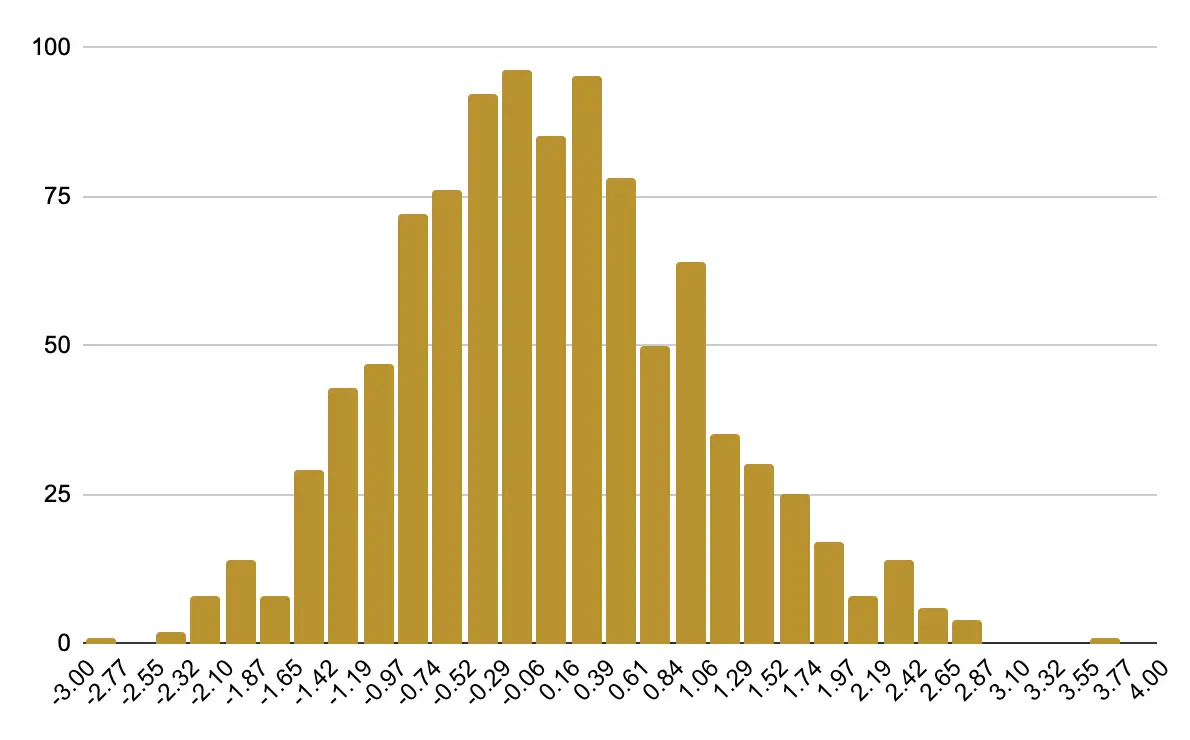
サンプル数1000のヒストグラム

サンプル数: 10000

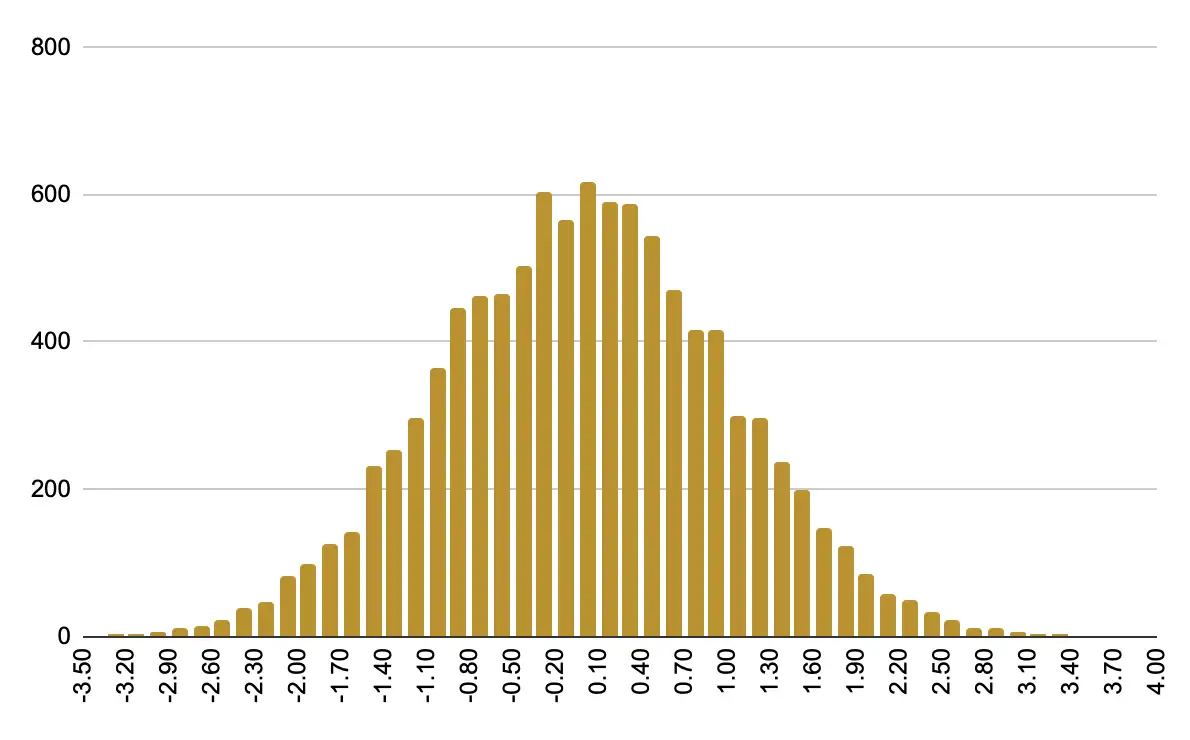
サンプル数10000のヒストグラム

サンプル数: 100000

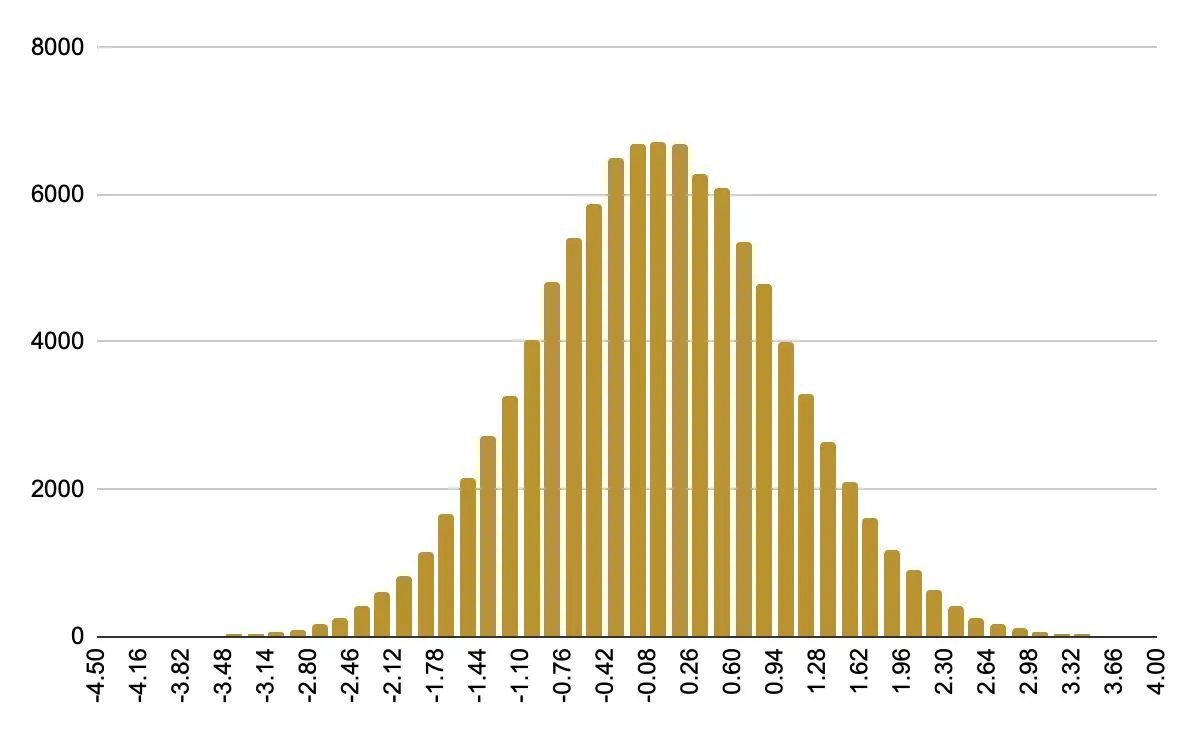
サンプル数100000のヒストグラム

正規分布で範囲を限定する

もしかしら、ある範囲の中で正規分布に従って乱数を生成したい、と思うことがあるかもしれません。範囲を絞っている以上は正規分布ではないのですが、作りたいプログラム上そういう要望があることもあると思います。

その場合、例えば以下のようにすると $\pm 3 \sigma$ に範囲を限定することができ、範囲指定と正規分布を兼ねたような乱数生成が可能です。

import random

def random_gauss_range(min_val, max_val, coef=3):
  mu = (min_val+max_val)/2
  sigma = (max_val-min_val)/(2*coef)

  while True:
    r = random.gauss(mu, sigma)
    if min_val <= r and r <= max_val:
      break

  return r

この sigma の式は以下のように求められます。

$$ \begin{aligned} \mu + {\rm coef} * \sigma &= {\rm maxval} \\ \sigma &= \frac{{\rm maxval} - \mu}{{\rm coef}} \\ &= \frac{{\rm maxval} - ({\rm minval} + {\rm maxval}) / 2}{{\rm coef}} \\ &= \frac{{\rm maxval} - {\rm minval}}{2 * {\rm coef}} \end{aligned} $$

さいごに

NumPyやSciPyなどのライブラリを使わずとも、Pythonの標準ライブラリであるrandomを使って標準偏差に従った乱数を生成することができます。ただし標準ライブラリを使う場合とNumPyなどの外部ライブラリを使う場合とで、乱数の質や実行速度に差がある可能性があります。性能にシビアな環境においてはよく検証した上で相応しいものを選択してください。