C言語で範囲を指定した乱数を生成する

C言語でプログラミングをする際、指定した範囲内での乱数が欲しい場面があります。 巷には単に最大値で剰余を取ればいいとしか解説していないものもありますが、それでは偏りのある乱数となる場合があります（それで問題無い場面も多いですが、問題無いかどうかは利用者が判断すべきことでしょう）。

今回はC言語で指定した範囲内での整数乱数を取得する方法を（単に剰余を取る方法も含め）いくつか紹介します。

C++11以降を使う場合はSTLで簡単に実現ができますので、以下の記事を参考にしてみてください。

C++で範囲を指定した乱数を生成する

rkd3.dev

範囲を指定した乱数を生成する方法

C++のSTLのような便利なライブラリを使用せず、地道に範囲を指定した乱数を得る方法を紹介します。 同様のアルゴリズムを実装できればどんな言語にも応用可能です。

前提：乱数を生成する方法

上で『ライブラリを使用せず』と書きましたが、乱数生成自体に関しては既に存在するものを利用することとします。

乱数生成関数と言えばC言語付属のrand関数が有名ですが、rand関数は乱数の質が悪いことでも有名です。 C++のSTLでも採用されているメルセンヌ・ツイスタを実装したライブラリを使用することをおすすめします。

メルセンヌ・ツイスタの開発者の一人である松本眞氏によりC言語用のライブラリが以下にて公開されています。

下記の記事にてrand関数とメルセンヌ・ツイスタの違いや、上記ライブラリの使い方などを解説しています。

C言語でのメルセンヌ・ツイスタライブラリ（SFMT）の使い方

rkd3.dev

以下では一様な乱数整数を返す関数としてgenrand()という関数が存在し，その生成しうる最大値がRANDMAXであることとします。そのままコピペしても動きませんのであしからず。

方法１：最大値で剰余を取る

まず、よく用いられる方法として範囲の最大値で剰余をとる方法があります。

0からmax_valの範囲の乱数が欲しい場合は

int get_rand(int max_val) {
    return (int)(genrand() % (max_val+1));
}

min_valからmax_valの範囲の乱数が欲しい場合は

int get_rand(int min_val, int max_val) {
    return (int)((genrand() % (max_val+1 - min_val)) + min_val);
}

とします。

問題点

この方法には得られる乱数に偏りがあるという特徴があり、範囲ごとに出現頻度がきっぱりと分かれます。

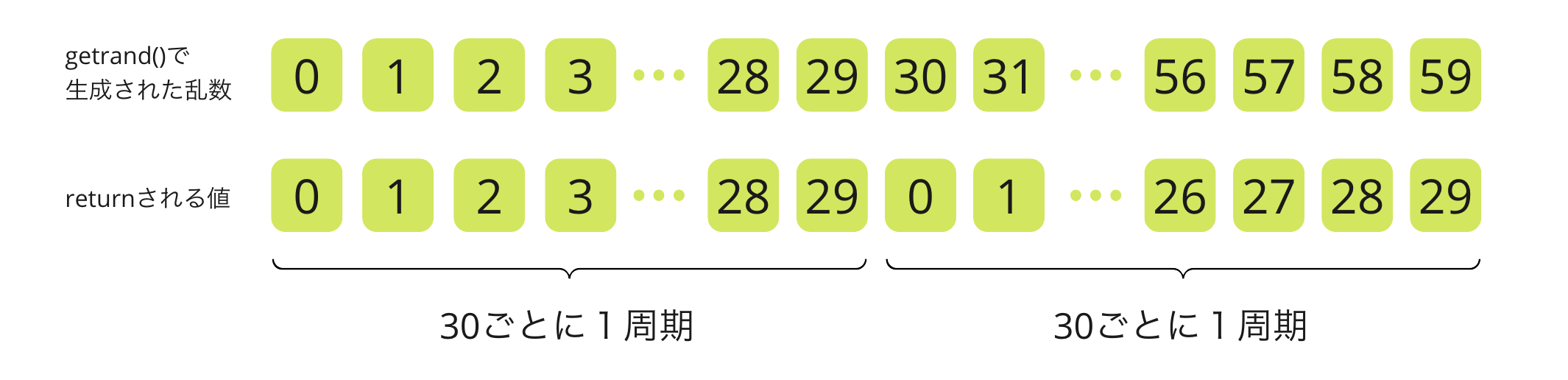
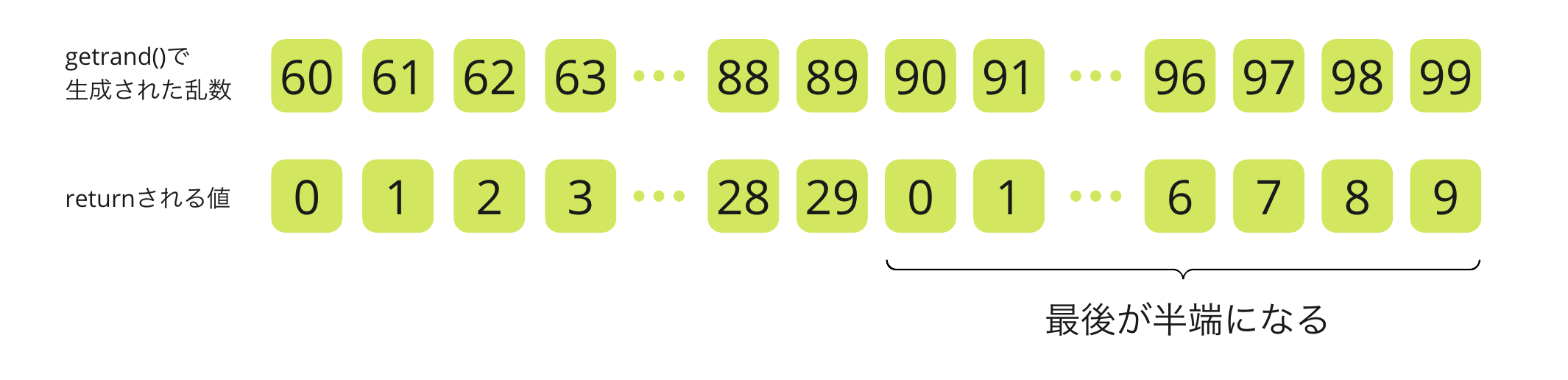
例として、仮にgenrand()の生成する範囲を0〜99、max_valを29としましょう。 すると、genrand()が0〜89を出力する場合は0〜29が均等に得られますが、genrand()が90〜99を出力する場合は0〜9の間しか得られません。つまり0〜9と10〜29で得られる確率が違います。この例だとそれぞれの範囲の値（例えば0と10）が出現する頻度の割合は10:9となります。つまり0は10より1割ほど出やすくなります。

方法２：乱数の最大値で割ってから範囲の最大値をかける

別のシンプルな方法として以下のような方法があります。

0からmax_valの範囲の乱数が欲しい場合は以下の通り。

int get_rand(int max_val) {
    return (int)(genrand() / ((double)RANDMAX+1.0) * (max_val+1));
}

min_valからmax_valの範囲の乱数が欲しい場合は以下のようにします。

int get_rand(int min_val, int max_val) {
    return (int)(genrand() / ((double)RANDMAX+1.0) * (max_val+1 - min_val) + min_val);
}

こちらの方法も手軽でわかりやすいのですが問題があります。

問題点

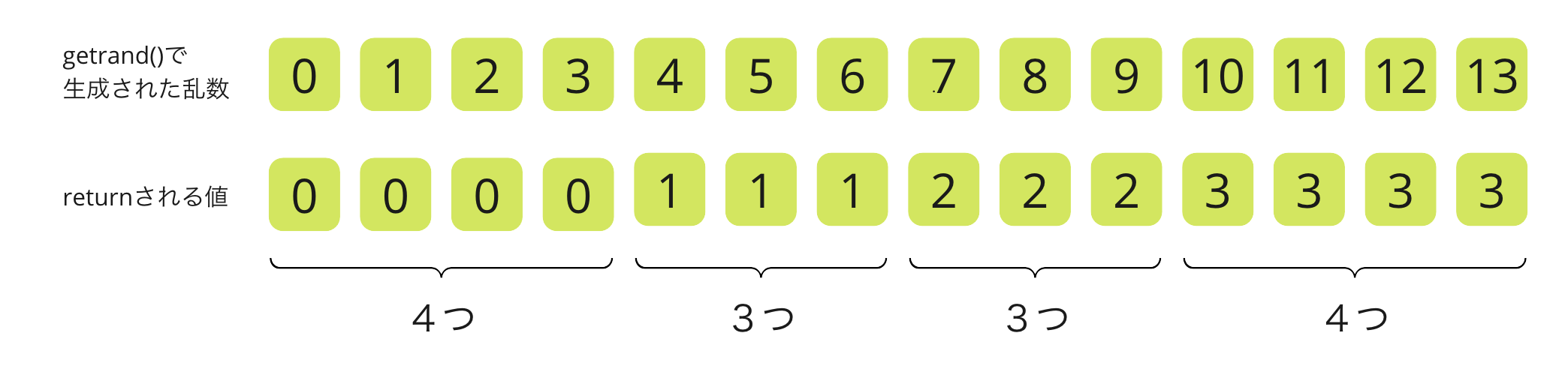
前述の例の通りgenrand()の生成する範囲を0〜99、max_valを29と仮定します。すると、genrand()が0〜3を出力する場合は結果が0、4〜6を出力する場合は結果が1となり、0が出る頻度と1が出る頻度の割合は4:3となります。つまり0は1より3割ほど出やすくなります。

方法１・２の補足

方法１と２の問題はRANDMAXがmax_valから見て十分に大きくない場合に発生する問題と言えます。逆にRANDMAXが十分大きい場合においては影響は小さくなります。

例えば、32bit整数の乱数（0〜4294967295）を生成できる場合、それを前者の剰余を取る方法によって0〜999の範囲に絞ると、0〜295の範囲の任意の値aが出る確率と296〜999の範囲の任意の値bが出る確率の比は4294968:4294967となります。 つまりaが出る確率とbが出る確率の差は約0.00002%です。この差をどう捉えるかは状況によりますが、これが無視できる程度であるという場面も少なくはないでしょう。

中には0.00002%の差すら許されない場面も存在するかと思います。 そのような厳密に偏りの無い一様な乱数が必要とされる場合は以下の方法３のようにします。

方法３

ここでは厳密に偏りの無い方法を紹介します。

int get_rand(int min_val, int max_val) {
    int randmax_limit = (int)(RANDMAX / (max_val+1 - min_val)) * (max_val+1 - min_val);
    int r;
    while ((r = genrand()) > randmax_imit);
    return (r % (max_val+1 - min_val)) + min_val;
}

方法１と２における偏りの原因はgenrand()で得られる値の幅がmin_valからmax_valの値の幅の整数倍になっていないことに起因します。つまり、genrand()で得られる範囲をmin_valからmax_valの値の幅の整数倍であるrandmax_limitに制限する（randmax_limit以下の値が出るまでやり直す）ことで、無理矢理一様になるようにしています。

もちろん、乱数ですのでこのwhileが終了する保証はありませんが、よほど質の悪い乱数生成器を使用しない限り問題になることは無いかと思われます。（whileの条件を満たす確率はmin_valとmax_valによりますが必ず50%未満となります。50%としても10回連続でwhileの条件を満たす確率が0.1%未満であることを考えれば、このループが問題になる場面はかなり限られるでしょう。）

まとめ

C言語で範囲指定した乱数の生成方法を紹介しました。また一般的な剰余を取る方法などでどのような問題があるかを解説しました。

簡単な方法で一見よさそうですが、意外と問題が潜んでいるというのはアルゴリズムの怖いところですね。

余談

アルゴリズムやデータ構造はプログラミングをする上で基本的な知識です。スタック、キュー、ソーティングなど基本を網羅的に学べる書籍としてはこちらがおすすめです。

新・明解C言語で学ぶアルゴリズムとデータ構造第2版

柴田望洋

amazon.co.jp

C言語をしっかりと学びたい人にはこちらの書籍がおすすめです。ある程度Cを使えるようになった後にもう少し深いところからしっかりと理解したいという場合にぴったりだと思います（つまりあまり初心者向けではないです）。新版というのも出ているようですが中身が違うみたいですね。

独習C 第4版: ANSI規格準拠

ハーバート シルト (著), トップスタジオ (翻訳)

amazon.co.jp